Continuing from image editing with Functors, we will now understand Applicative by editing images with it.

Applicative

An applicative is composed of 2 things:

1. A function which can wrap any value A with the context F. pure(a: A): F[A]. So it must be that pure knows what the F context means.
2. One of the two functions which are equivalent to each other (can rewrite one in terms of the other + pure):
   • map2(a: F[A], b: F[B], f: (A, B) => C): F[C]
   • app(f: F[A => B], a: F[A]): F[B]

Below app is used with the enhanced syntax:

fab.app(a: F[A]): F[B]
//where fab is of type F[A => B]

This structure must obey the laws:

• identity

F.pure((a: A) => a).ap(fa) == fa

• Homomorphism

F.pure(f).ap(F.pure(a)) == F.pure(f(a))

• Interchange

ff.ap(F.pure(a)) == F.pure((f: A => B) => f(a)).ap(ff)

• Composition

val compose: (B => C) => (A => B) => (A => C) = _.compose
F.pure(compose).ap(fbc).ap(fab).ap(fa) == fbc.ap(fab.ap(fa))

These laws are a bit complicated, so again like Functors we will check them with Cats laws. The tests are more fine grained than only these 4 laws so if some fail we will get a better idea what and where to fix.

checkAll("Applicative laws", ApplicativeTests(Image.imApplicative).applicative[Int, Int, String])

Map2

map2(a: F[A], b: F[B], f: (A, B) => C): F[C]`

This says it can merge two contexts. The f function knows how to merge A and B into a new value C, but map2 knows (just like pure) about what the F context means, so it actually knows to merge both contexts together. We can replace the word “context” with “effect”: map2 knows how to merge two effects.

Apply

app(f: F[A => B], a: F[A]): F[B]

This is more tricky to understand intuitively but given a function/program wrapped in the context/effect F, we can run the program with the value in a: F[A]. Not to be confused with the functor’s map(a: F[A], f: A => B): F[B] - there is an extra F over f in apply.

Because apply also gets as input two Fs and returns only one it means that it also knows how to merge these Fs (just like map2)

Map2 vs Apply

So what is the difference? Formally none because we can write one in terms of the other + pure

def map2[F[_], A, B, C](fa: F[A], fb: F[B], f: (A, B) => C): F[C] = {
  val one = ap(pure(f curried))(fa)
  ap(one)(fb)
}

def apply[A, B](ff: F[A => B])(fa: F[A]): F[B] =
  map2(ff, fa)((f, a) => f(a))

So it’s clear that both map2 and apply know how to merge F contexts/effects, but what about the difference in signatures?

ff: F[A => B] from apply is the partial application of f: (A, B) => C from map2 with a: F[A]. It kinda holds a F[A] inside. More precisely it’s a program which ran with input A will produce a F[B]. We’ll see this below on images.

Applicative is also a Functor

The complete name is: applicative functor.

def map[A, B](fa: F[A])(f: A => B): F[B] =
  ap(pure(f))(fa)

But functor is not an applicative, functor does not have pure so it does not know as much about what F means.

Applicative on images

implicit val imApplicative: Applicative[Image] = new Applicative[Image] {
    override def pure[A](x: A): Image[A] = new Image[A]({
      _: Loc => a
    })

    override def ap[A, B](ff: Image[A => B])(fa: Image[A]): Image[B] = {
      new Image[B]( loc => 
        ff.im(loc)(fa.im(loc))
      )
    }
}

Given F is an Image it means we can combine any 2 images, pixel by pixel. Of course, if we can combine 2 images we can also combine any N images.

Original image A:

Original image B:

Max brightness between A and B

def max(a: Image[Color], b: Image[Color]): Image[Color] =  
  a.map2(b) {  
    case (a, b) => if (a.brightness > b.brightness) a else b  
  }

See through white

def overlapIf(imga: Image[Color], imgb: Image[Color], f: Color => Boolean): Image[Color] = {
  val effect: Color => Color => Color = a => b => if (f(b)) a else b
  val ap1 = imApplicative.ap(imApplicative.pure(effect))(imga)
  val ap2 = imApplicative.ap(ap1)(imgb)
  ap2
}
overlapIf(bird, crayons,  c => c.isWhiteish)

Disolve (creates a new image randomly taking color from A or B)

overlapIf(bird, crayons,  _ => Math.random() > 0.5)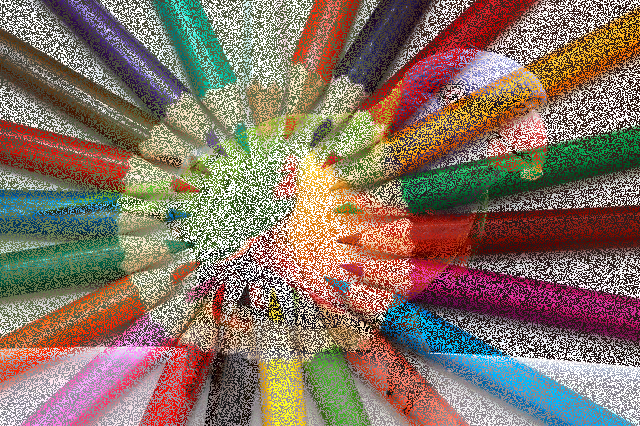

Recolor

a.map2(b) {
  case (a, b) =>
    Color(a.brightness * b.red, a.brightness * b.green, a.brightness * b.blue)
}

Getting more intuition on Map2 and Apply

We define a program in our F (Image), which will generate a checkers-like pattern.

    def checkerPattern: Image[Color => Color] = {
      new Image[Color => Color](
        loc => c => loc match {
          case Loc(a, b) =>
            if (a % 10 < 5 && b % 10 < 5) Color.White
            else if (a % 10 >= 5 && b % 10 >= 5) Color.Black
            else c
        }
      )
    }

We will run this program giving it as input the original bird image, and we get

ap(checkerPattern)(bird)

Now let’s create the same result with map2.

map2(bird, checkerPattern)((a, b) => b(a))

I’m going to repeat myself because this is awesome:
ff: F[A => B] from apply is the partial application of f: (A, B) => C from map2 with a: F[A], it kinda holds a F[A] inside. We can even extract this core image from our checkerPattern program in order to see it by giving it the transparent color:

checkerPattern.map(c => c(Color.Clear))
//OR
ap(checkerPattern)(pure(Color.Clear))

And one more fun example, combined with the bird image:

    def psychedelics: Image[Color => Color] = {
      new Image[Color => Color](
        loc => c => loc match {
          case Loc(a, b) => Color(
            (1f * Math.sin(a / 20) + b / 300).toFloat,
            c.green,
            (1f * Math.cos(b / 40) + a / 150).toFloat,
          )
        }
      )
    }

    ap(psychedelics)(bird)

And the core image embedded in the F[A => B]

In the next post of this series we will see new capabilities implemented with the help of monads.